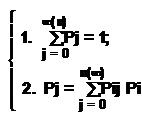Марковские цепи. Свойства и основные характеристики однородных марковских цепей.

Простейшим видом марковской цепи является однородная марковская цепь, в которой вероятности перехода из состояния в состояние P_ij не зависят от времени, а следовательно марковская цепь для любых сечений случайного процесса представляется одним и тем же G, одной и той же таблицей T.

Некоторые определения, которые позволят сформулировать свойства однородных марковских цепей /для рассчета и анализа в процессах /.

 

ОПРЕДЕЛЕНИЕ 1	Если в одной марковской цепи можно из любого состояния Zi перейти в любое другое состояние за как угодно большой интервал времени, то такая марковская цепь называется неприводимой. В графе такой марковской цепи будут отсутствовать "висячие" вершины /в которые входят стрелки, но не выходят/.
ОПРЕДЕЛЕНИЕ 2	Состояние однородной марковской цепи Zj называется возвратным, если вероятность вернуться в него по истечении некоторого большого времени равна 1.
ОПРЕДЕЛЕНИЕ 3	Средним временем возвращения  в некоторое возвратное состояние Zj называется среднее время между многими очередными возвращениями в это состояние. Если имеет место цикличность, то тогда речь идет о стахастическом процессе, а можно использовать более простые средства анализа.
ОПРЕДЕЛЕНИЕ 4	Если все состояния однородной марковской цепи апериодичные, то такая марковская цепь называется апериодической, и в ней не развиваются различные циклические процессы.
ОПРЕДЕЛЕНИЕ 5	Если времена возвращения trj не одинаковы /не повторяются/, то такое возвратное состояние Zj называется опериодичным.

 

СВОЙСТВО 1:

Если марковская цепь однородна, неприводима и апериодична, то для каждого состояния цепи существуют некоторые предельные вероятности состояний P_j, которые называются равновесными, и которые не зависят от времени и от начальных условий, т.е.

Вероятностный переходный процесс как-бы закончился и наступил равновесный, не зависящий от P_j (0).

СВОЙСТВО 2:

 Если все состояния однородной марковской цепи возвратны, а средние времена t_rj конечны, то для такой марковской цепи имеет место стационарное распределение вероятностных состояний:

- сумма произведений другого состояния на вероятность перехода из i-го состояния в j-тое

Равновесие вероятности состояний марковской цепи и вероятности переходов позволяют вычислить важные характеристики однородного марковского процесса:

- время возвращения в j-тое состояние - среднее время пребывания в каждом j-ом состоянии

Но эти времена задаются с учетом шага испытаний .

Текущее состояние процесса на марковском графе отображается точкой. На каждом шаге  мы точку снимаем и разрываем переход. Среднее время возврата в каждое состояние:

 выбирается как минимальный шаг, при котором возможен физический переход.

Для определения среднего времени  воспользуемся некоторыми фрагментами цепи, которые подвергались испытаниям на каждом шаге.

Среднее время будет видимо определяться вероятностью переходов в то же самое состояние P_jj, которая должна согласовываться с вероятностью выхода / I- P_jj /.

Среднее время пребывания в j-том состоянии может определить как геометрическое расределение вероятности возвращения в то же состояние на k шагах испытаний. В этом случае вероятность того, что в Z_j будем находить k шагов будет:

Это геометрическое дискретное распределение характеризует результаты испытаний с /k-I/ неуспехом и одним успехом, и наоборот.

Для среднего времени при геометрическом распределении:

,

 

  - задает среднее время для k.

Геометрическое распределение является простейшим распределением без последствия. Именно оно характеризует процесс обследования заявок в СМО, поскольку Z_j мы можем рассмотреть как состояние обследования j-той заявки. Тогда среднее время ее обследования распределяется геометрически.

Если выходной поток СМО имеет более сложное распределение чем экспоненциальное или геометрическое, а для описания процессов СМО используется однородная марковская цепь, то в этом случае имеет место некоторое логическое несоответствие, и такая модель называется полумарковской. Такая модель называется с вложенным марковским процессом.

Если же выходной поток простейший, то можно назвать эту модель марковской и использовать однородные цепи для анализа процесса.